La solución al desafío matemático de la Lotería de Navidad 2016
Adolfo Quirós Gracián, profesor de la Universidad Autónoma de Madrid, resuelve el problema planteado a los lectores de EL PAÍS
Ya hay solución para el desafío matemático extraordinario de Navidad presentado por EL PAÍS y la Real Sociedad Matemática Española con motivo del sorteo de la lotería. Adolfo Quirós Gracián, profesor de la Universidad Autónoma de Madrid y director de La Gaceta de la RSME presentó el desafío y nos da ahora la solución.
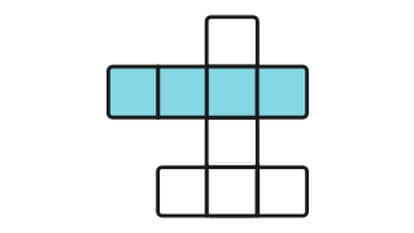
Recordemos que el desafío consistía en decir cuál es el número mínimo de cortes necesario para separar los mxn décimos de un megabillete de lotería, y explicar por qué ese número es mínimo y cómo proceder para separar los décimos con ese número de cortes.
La respuesta es que, no importa cómo lo hagamos, siempre vamos a necesitar mxn-1 cortes, con lo que ese número será también el mínimo. Pero hay que explicar el por qué.
Para ello basta con observar que empezamos con todos los décimos juntos. Tras el primer corte, lo hagamos como lo hagamos, tendremos dos piezas, tras el segundo corte, sin importar de nuevo cuál sea, tres piezas, y así sucesivamente: después de cada corte tendremos una pieza más. Como empezamos con una sola pieza (el megabillete) y al final tenemos mxn (cada uno de los décimos), habrá sido necesario realizar mxn-1 cortes.
Se han recibido 444 respuestas en el plazo marcado, pero no todas ellas podemos considerarlas completas. Hay quien no da ninguna justificación, quizás por considerar obvio el resultado, pero lo más frecuente en las soluciones que consideramos incompletas es decir que la forma óptima de hacerlo es separar primero digamos las filas, lo que requiere m-1 cortes, y luego separar en décimos las tiras largas así obtenidas, lo que se necesitan n-1 cortes por tira. La cuenta final es entonces m-1+ m x(n-1)=mxn-1.
De quienes hacen esto (un 48% del total de respuestas) unos comparan "los dos procedimientos posibles, empezar por separar las filas o por separar las columnas" y al obtener lo mismo concluyen que es lo óptimo, otros señalan que "lo óptimo tiene que ser hacer los cortes más largos posibles", y algunos dan otros argumentos, siempre con la misma idea. Pero no es evidente que hacer cortes largos sea mejor (de hecho, ahora sabemos que es igual que cualquier otro orden de corte) y usando otro principio que con frecuencia funciona (las soluciones óptimas son simétricas) se podía haber argumentado que lo óptimo era intentar quedarse con bloques "cuadrados", con dxd décimos.
Esta idea, quedarse con bloques cuadrados y además pedir que d sea potencia de 2, ha sido la que han utilizado algunos del pequeño número de lectores que se han tomado las normas demasiado al pie de la letra y, poniendo bloques en paralelo (lo que es cierto que no mencionamos explícitamente como prohibido, pero es equivalente a apilar) o sometiendo a los megabilletes a diversos giros, han atacado un desafío mucho más complicado que el que teníamos en mente. Quizás el caso más espectacular es el de Manuel Aarón F. G, quien desde Estados Unidos nos envía una ingeniosa manera de cortar retorciendo el megabilete (aunque nos faltan manos para hacerlo si el billete es grande).
La suya es un ejemplo de las respuestas recibidas desde al menos diez países en América, Asia y Europa. Una de ellas, absolutamente correcta, la ha enviado un grupo de estudiantes de Guadalupe, en las Antillas Francesas, que han utilizado el desafío tanto en su clase de matemáticas como en la de español.
Ellos argumentan esencialmente como hemos hecho arriba, pero lo presentan usando inducción. La mayoría del 29% de respuestas correctas y completas lo hace así (con o sin inducción), pero hay quien utiliza otras maneras de exponerlo. Por ejemplo, Miguel Ángel O. C. lo hace presentando un árbol de decisión. También hay quien, como Sergio G., observa que se podían admitir cortes en zig-zag, siempre que cada corte divida un bloque de décimos en dos.
La RSME ha decidido enviar un ejemplar del libro Gardner para principiantes a tres lectores seleccionados por la sociedad de entre quienes han enviado respuestas consideradas completas. Son Gonzalo U., Goyo L. y Tania N.
Hayáis dado o no con la respuesta, esperamos que hayáis pasado un buen rato con este desafío, que me sugirió, con tabletas de chocolate en lugar de billetes de lotería, mi colega Luca Fanelli, de la Università di Roma 1 La Sapienza (esa versión con tabletas de chocolate la han mencionado también algunos lectores). Como señala otro lector, Sergio de M., el desafío era en principio técnicamente más sencillo que otros anteriores y la "dificultad" estaba en lo sorprendente del resultado.
En nombre de EL PAÍS, de la RSME y en el mío propio, os deseo felices fiestas.
[Aquí puedes ver todos los desafíos anteriores]